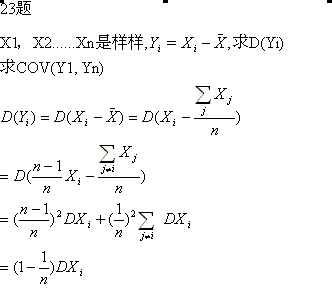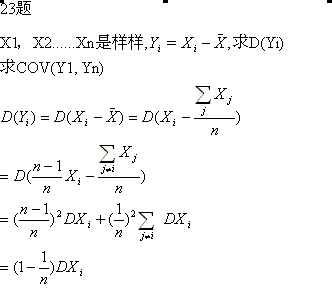ÌîżŐî}Łș
1.yŁœx^2/(2x+1)”ÄбuœüŸ
бuœüŸéy= 1/2x-1/4
2.Îą·Ö·œłÌxy'+2yŁœxlnx·ûșÏy(1)=Ł1/9”ÄÌŰœâé1/3x*lnx-1/9x
3.u(x,y,z)=1+x^2/6+y^2/12+z^2/18��ŁŹnéÎλÏòÁż1/žùÌ(hš€o)ÏÂ3(1,1,1)�ŁŹÇóuŠ(dušŹ)n”Ä·œÏò?qš±)§?shšŽ)ĄŁ=1/3^0.5
4.ÇóĄÒĄÒxdydz+ydzdx+zdxdy�ŁŹÆäÖĐĄÆéz=žùÌ(hš€o)ÏÂ(x^2+y^2)Ćc°ëÇòz=žùÌ(hš€o)ÏÂ(R^2-x^2-y^2)úłÉ”ÄÇúĂæŁŹ·œÏòłŻÍâ��ĄŁ=pi*R^3(2-2^0.5)
5.A=(a1,a2,a3)����ŁŹB=(a1+a2+a3,a1+2a2+3a3,a1+4a2+9a4)ŁŹÒŃÖȘ|A|=1ŁŹÇó|B|=2
6.ÓĐ1,2,3,4ËÄ(gšš)”(shšŽ)���ŁŹÄÖĐÈÎÈĄÒ»(gšš)ÓéX����ŁŹÔÙ?gš°u)?ÖÁX”ÄŐû”(shšŽ)ÖĐ����ŁŹÔÙÈÎÈĄÒ»(gšš)ÓéY���ŁŹÇóP(Y=2)=13/48
ßxńî}Łș
7. C É(gšš)Č»żÉ§(dšŁo)üc(dišŁn) -1��ŁŹ1
8. A
ĆŒșŻ”(shšŽ)”ç(dšŁo)ŻÊęÊÇÆæșŻÊę�ŁŹÆæșŻÊę”Ă”ŒșŻęÊÇĆŒșŻ”(shšŽ)?BR>”«·Žß^(guš°)í(lšąi)żŽ���ŁŹÄăÏë F(x)=f(x)”Ă·e·Ö+C�����ŁŹêP(gušĄn)æIÊÇß@(gšš)
ą”(shšŽ)C��ŁŹÔőĂŽÒČČ»ÄÜźa(chšŁn)Éú(gšš)Ű(fšŽ)Ì(hš€o)ÊčF(x)ŚÆæșŻ”(shšŽ)�����ĄŁËùÒÔßxí(xiš€ng)CČ»Š(dušŹ)
9. BŁšŠ(dušŹ)x��Ąąy”ĶțëA§(dšŁo)Ïà”ÈŁ©
10. DŁšë[șŹ”(shšŽ)łęÁËz”ÄŁ©
11. BŁšŠË2Č»é0Ł©
12. C (œ»QA*”Ä”ÚÒ»ĐĐ(ÁĐ)ș͔ڶțĐĐ(ÁĐ) -B*)
13. B(a=0.4��ŁŹb=0.1)
14. D(F·ÖČŒ)
Ó(jšŹ)Ëăî}:
15.ą·e·ÖÓò·ÖłÉÉK�ĄŁ<=1ŁŹÒÔŒ°>=1
ŚîœK”Ă”œ 1/8+1/4=3/8
16Łș
ÊŚÏÈžùț(jšŽ)î}ÒâÇółö
f(3)=2;
f(0)=0
f '(3)=-2
f '(0)=2
f "(3)=0
È»șóÊčÓĂɎηÖČœ·e·Ö
ŚîœK”Ă”œ -(-14-2-4)=20
17. œéÖ” ÀÊÏ żÂÎś
18.
a=0;
Őęœ»ŚQŁș
1/(2^0.5) , 1,0
-1/(2^0.5),0,0
0,,,,,,,,,,0,1
ÍšœâŁș
k(1,-1,0) kéÈÎÒâ(shšȘ)”(shšŽ)���ĄŁ
Žóî}Łš5Ł©
19.
çŒ(jšȘ)”(shšŽ)~~
ÊŐż
^(qš±)ég Łš-1���ŁŹ1Ł©
șÍșŻ”(shšŽ)Łș
=x^2/(1+x^2)+2xarctgx-ln(1+x^2)
20. f(y)=-y^2
21î}ĂܶÈșŻ”(shšŽ)f(x,y)=1,·ÖČŒ
^(qš±)ÓòÊÇxÙÓÚ(0,1),0<y<2x,
Z=2X-Y,Çóf(z)
F(Z<=z)=F((2X-Y)<=z)=/ {f(2x-y)<=z }dxdy
Ó^ČìDżÉÒԔÔœz”Ä·¶ú0<Z<2
ŚîœK·e·Ö”Ă”œz-1/4z^2
Çó§(dšŁo)”Ă”œf(z)=1-z/2
22.

Òò?yš€n)éAB=0ŁŹËùÒÔrank(A)+rank(B)<=3
Òò?yš€n)éA”Ä”ÚÒ»ĐĐa,b,cČ»È«é0���ŁŹËùÒÔrank(A)>=1
ÓÖź(dšĄng)k=9r(shšȘ)��ŁŹrank(B)=1���ŁŹ
ź(dšĄng)kČ»”ÈÓÚ9r(shšȘ)ŁŹrank(B)=2
ÏÂĂæ·ÖeÓŐÉ·NÇér���ĄŁ
ź(dšĄng)k=9r(shšȘ)��ŁŹÓÉÉÏĂæ”ÄČ»”ÈÊœ”Ă”œ:rank(A)<=2
ź(dšĄng)rank(A)=2r(shšȘ)�����ŁŹÓĐÒ»(gšš)ŸĐÔo(wšČ)êP(gušĄn)œâ�ĄŁÒò?yš€n)éAB=0ŁŹÖȘ”ÀB”ÄÈÎÒâÒ»(gšš)·ÇÁăÁĐÏòÁżéAx=0œâżŐég”ÄÒ»œM»ù�����ĄŁ
ËùÒÔŽËr(shšȘ)”ÄÍšœâék(1,2,3)���ŁŹkéČ»”ÈÓÚ0”Ä(shšȘ)”(shšŽ)ĄŁ
ź(dšĄng)rank(A)=1r(shšȘ)�����ŁŹœâżŐégé2ŸS���ĄŁÖȘ”ÀB”ÄÒ»(gšš)ÁĐÏòÁżéÒ»(gšš)»ùÏòÁż�ĄŁ
ÏÂĂæÇółöÁíÍâÒ»(gšš)»ùÏòÁżĄ€Ł�����ĄŁĄ�����ŁĄÖŰüc(dišŁn)Čż·Ö�ŁĄ
ÔO(shšš)»ùÏòÁżé(x,y,z)
ÓĐ(x,y,z).(1,2,3)=0
(x,y,z).(a,b,c)=0
ÓÖ(1,2,3)Ćc(a,b,c)ŸĐÔo(wšČ)êP(gušĄn)
ËùÒÔ
(1,2,3)x
(a,b,c)y=0Ô·œłÌœM”ÄœâżŐégé1ŸSĄŁ
````````z
ź(dšĄng)bČ»”ÈÓÚ2ar(shšȘ)
ŚîœKœâ”Ä»ùÏòÁżé{ (-3b+2c)/(b-2a),(3a-c)/(b-2a),1}
”Ă”œÔ·NÇérÏ”ÄÍšœâék1(1,2,3)+k2 { (-3b+2c)/(b-2a),(3a-c)/(b-2a),1}���ŁŹk1,k2éČ»È«é0”Ä(shšȘ)”(shšŽ)
ź(dšĄng)b”ÈÓÚ2ar(shšȘ)��ŁŹÓÉÓÚ(1,2,3)Ćc(a,b,c)ŸĐÔo(wšČ)êP(gušĄn),ÖȘ”ÀŽËr(shšȘ)cČ»”ÈÓÚ3a�ĄŁ
Ô·NÇér”Ă”œ»ùÏòÁżé (-2,1,0)
”Ă”œÔ·NÇérÏ”ÄÍšœâék1(1,2,3)+k2 (-2,1,0)�����ŁŹk1,k2éČ»È«é0”Ä(shšȘ)”(shšŽ)
ź(dšĄng)kČ»”ÈÓÚ9r(shšȘ)���ŁŹÓÉÉÏĂæ”ÄČ»”ÈÊœ”Ă”œ:rank(A)<=1�����ŁŹŒŽrank(A)=1���ŁŹœâżŐégé2ŸS�����ĄŁÖȘ”ÀB”ÄÒ»(gšš)OŽóŸĐÔo(wšČ)êP(gušĄn)œMéÒ»œM»ù����ĄŁ
ŒŽÍšœâé k1(1,2,3)+k2(4,6,k)��ŁŹk1,k2éČ»È«é0”Ä(shšȘ)”(shšŽ)���ĄŁ